Video Summary

1.Project Summary

Solve an intricate maze with traps, lava, etc. Optimize by trying to improve the time the agent solves the maze or by finding the most optimal path. The input of the project would require a section of the map the agent would traverse. Output would be the most optimal path discovered by the agent. Lastly, we assume that every block is unknown and the agent must discover each path. Direct applications of this project would allow users to optimally beat multiple video games. At a high level, reinforcement learning discovered from this project can determine the ideal behavior within the manufacturing, delivery, and finance industries.

Level 1: Flat terrain, with edge boundary (Actions: Walk, Jump)
Level 2: Flat terrain, with edge boundary and hazards in the middle of the map (Actions: Walk, Jump)
Level 3: 3D terrain, hills, hazards, blocks (Actions: Walk, Jump)
Level 4: 3D terrain, hills, hazards, blocks (Actions: Walk, Jump, Timed Jump)
Level 5: Moonshot case- 3D terrain, hills, hazards, blocks and zombies (Actions: Walk, Jump, Timed Jump)

2.Approach

For progress report, our approach used the Q-Learning algorithm. Here is the equation of Q-Learning algorithm and our parameter set-up.
The Q-Learning equation:

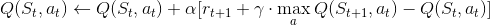
self.epsilon = 0.01 # chance of taking a random action instead of the best
self.alpha = 0.1 # learning rate
self.gamma = 1.0 # discount rate

# Set of actions
self.actions = ["movewest 1", "moveeast 1", "movenorth 1", "movesouth 1", "jumpnorth 1", \
                        "jumpsouth 1", "jumpwest 1", "jumpeast 1"]
#Action cost = 1 + self.action_cost[i]
self.action_cost = [0, 0, 0, 0, 9, 9, 9, 9]

#Initial Q Values (this snippet is used everytime agent discovers a new area in the map)
if not self.q_table.has_key(current_s):
  self.q_table[current_s] = [0, 0, 0, 0, -2, -2, -2, -2]

Learning Rate: Alpha represents the learning rate. It is value between 0 and 1 ( 0 < a < 1). It indicates how much the utility values will be updated every time the agent takes an action. alpha = 0 means the agent will not learn anything. alpha = 1 means the agent will not consider any feature states (the agent only consider most recent information). In stochastic environment, alpha is preferable closer to 0 than 1. In our approach, we decide alpha value to be 0.1

Discount Factor: Gamma is the discount factor. It determines the importance of future information. Gamma closer to 0 will encourages the agent to seek out rewards sooner rather than later. It makes the agent assign a smaller reward to the feature action. Gamma closer to 1 will makes the agent seek for high reward in the feature. This value usually closer to 1. We set gamma value to 1 in our approach

Random Action: Epsilon is the possibility of taking a random action instead of the best one.
Immediate Reward Valuer: r is the immediate reward value
Max Q Value: The action has the highest utility value in next state will become the new Q value of that states

Initial Q Values We decided to give each state 8 initial Q Values where the first 4 values are 0 and the last 4 are -2. These values were set to make the agent prefer walking over jumping initially until walking’s Q value drops to -2.

Note: Notice how each action costs 1 by default. We decided to creat an action_cost array to add additional cost to specific actions. A ‘jump’ has an additional cost of 9 on top of the default cost of 1 whereas a ‘move’ has no added cost.

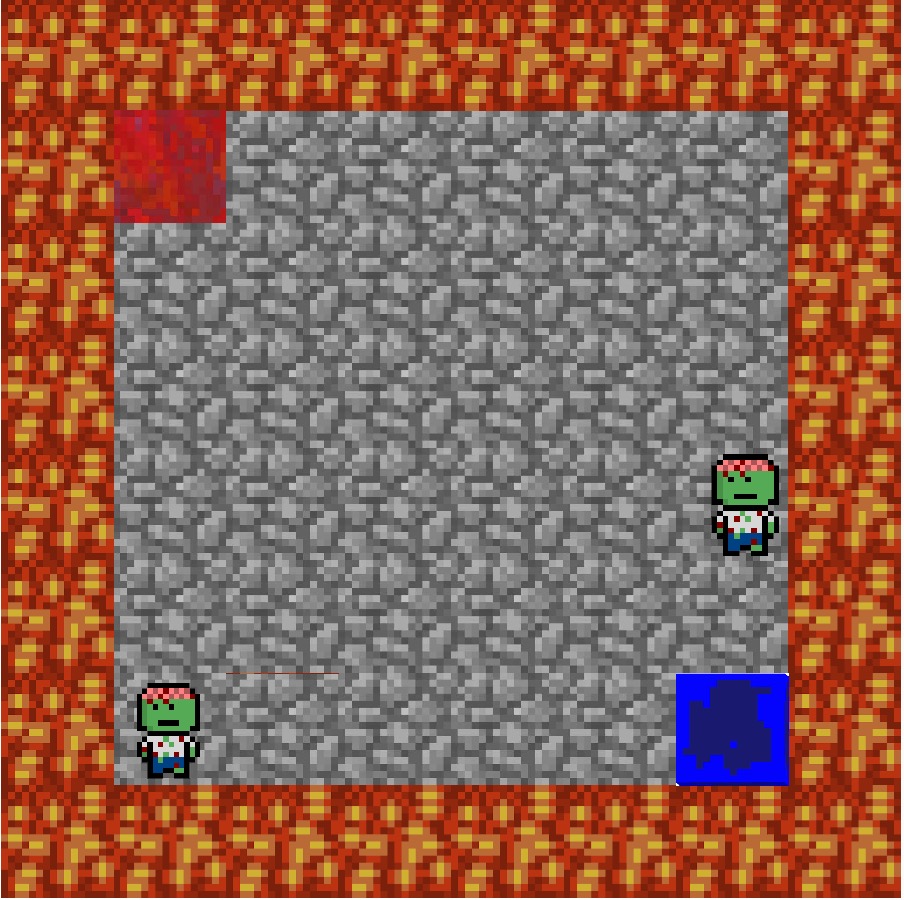
The 3 Levels

The Figure shows the grid layout in two-dimensional. It specify the start and end blocks. Also，it shows the terrian of mazes(the floor of the maze is cobblestone, block is built by glass_blocks, hill is built by cobblestone_blocks). The number in each grid represent the (x,z) value and each grids has an altitude value which is y.

Currently, we have three maps, each one is based on the previous one.

Level 1:

The level 1 map is a flat terrain with lava on eages. It is a 7x7x1(LxWxH) grid. The agent start at the lapis_block and try to reach the redstone_block. The agent can either walk or jump. In level 1, there are () states and 2 actions

Level 2:

The level 1 map is built based on Level 1 map. 5 cobble stone blocks in the middle of map were replaced by 5 lava blocks.It is a 7x7x1(LxWxH) grid. The agent start at the lapis_block and try to reach the redstone_block. The agent can either walk or jump. In level 2, there are () states and 2 actions

Level 3:

Level 3 map was built based on level 2 map. A 2x2x2(LxWxH) glass block and a 2x2x1(LxWxH) cobble stone hill. Agent can jump over the cobble stone block(gold) but cannot jump over the glass block. The agent start at the lapis_block and try to reach the redstone_block. The agent can either walk or jump. In level 1, there are () states and 2 actions

Reward for each actions:

For each action the agent makes, there is a reward value of -1 for each move, -10 for each jump, -100 for reaching the lava block, +100 for reaching the redstone_block(goal state)

3.Evaluation

For qualitative evaluation, we evaluate our project by checking how well the agent can solve all 3 level mazes. We observe the agent when it is solving the maze to verify it works correctly. Also, we can check our agent by using the Cumulative Rewards Table.

Level1: one of the optimal path of level 1 is (1,1) move-> (1,2) move-> (1,3) move-> (1,4) move-> (1,5) move-> (1,6) move-> (2,6) move-> (3,6) move-> (4,6) move-> (5,6) move-> (6,6). It takes 10 moves. Therefore, the best reward we can get is 90. The Cumulative Rewards Table shows how the agent successfully finds the solution with the highest reward.

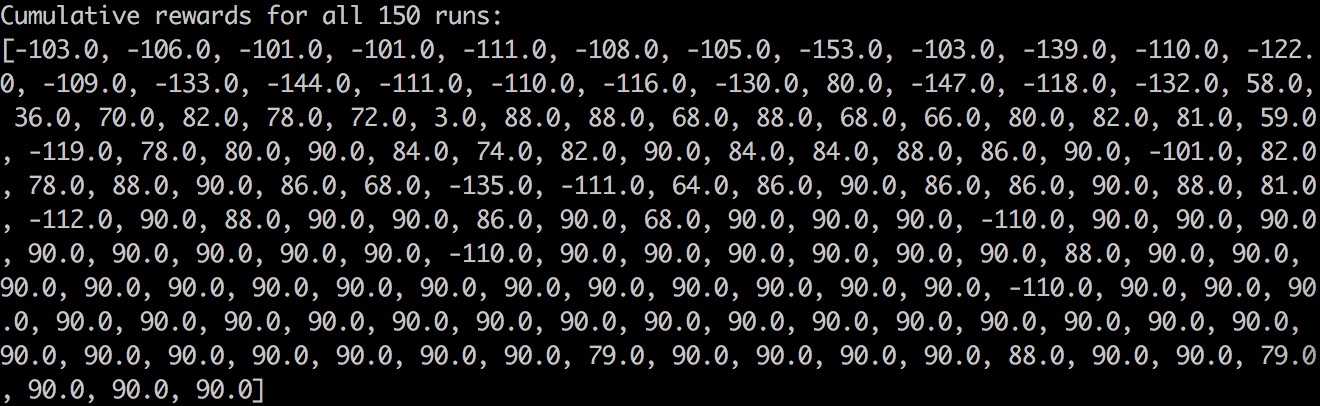
Level2: one of the optimal path of level 2 is (1,1) move-> (2,1) move-> (2,2) move-> (2,3) move-> (3,3) move-> (4,3) move-> (5,3) move-> (5,4) move-> (5,5) move-> (5,6) move-> (6,6). It also takes 10 moves. Therefore, the best reward we can get is 90. Here is the Cumulative Rewards Table of level 2. The agent successfully finds the solution with the highest reward in level 2.

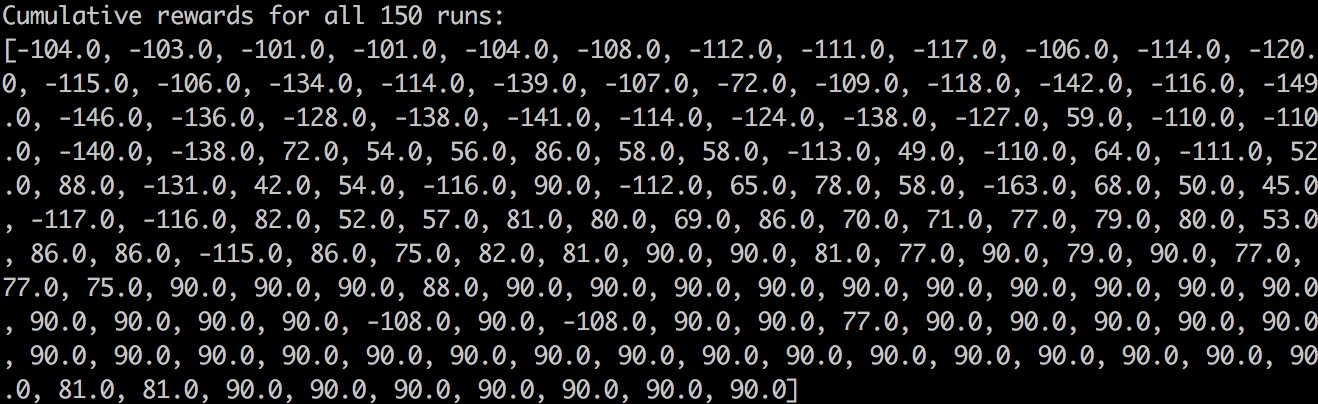
Level3: one of the optimal path of level 3 is (1,1) move-> (2,1) move-> (2,2) move-> (2,3) move-> (3,3) moves-> (3,4) jump-> (4,4) move-> (5,4) move-> (6,4) move-> (6,5) move-> (6,6). It takes 10 moves. However, from (3,4) to (4,4) the agent takes the action “JUMP” witch takes 10 rewards. Therefore, the best reward is 100 - 10 - 9 = 81. Here is the Cumulative Rewards Table of level 3. The agent successfully finds the solution with the highest reward in level 3.

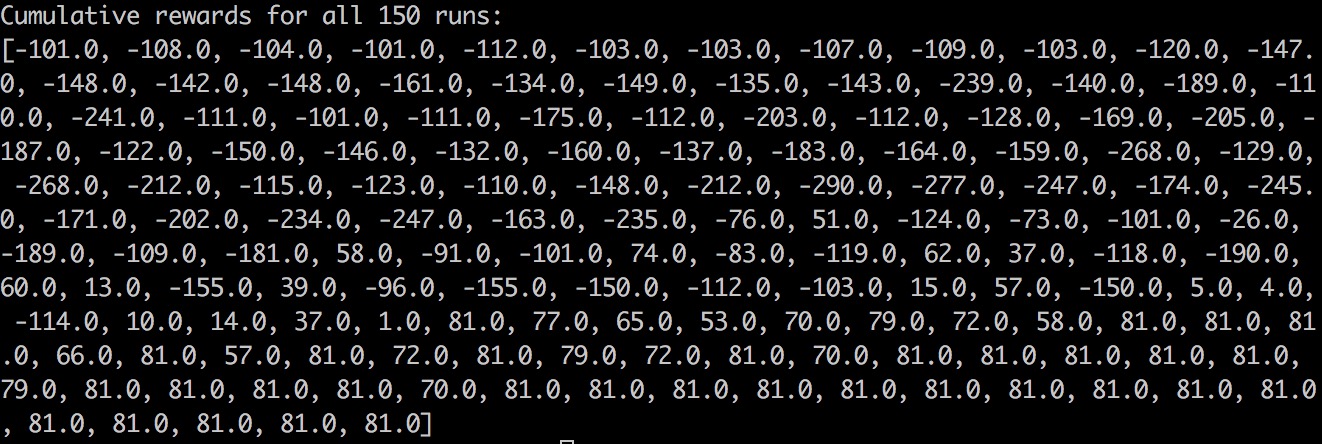
In terms of quantitative evaluation, we evaluate our project by checking how long it takes the agent to solve each mazes. That is, we want the agent to slove the maze as quick as it can. We use the Cumulative Rewards Table to check how many runs it takes before getting the best reward. In the most recent test, the agent needs 44 runs in level 1, 56 runs in level 2 and 104 runs in level 3. We hope we can improve this by changing our reward function and Q-Learning parameter. We want to see how changes on these parameter can affect agent’s performance.

| Tables        |    level 1    |    level 2     |    level 3    |
| ------------- |:-------------:| :-------------:|:-------------:|
| # of runs     |      44       |       56       |      104      |

4.Remaining Goals and Challenges

For the rest of weeks, we will add a “timed jump” which means the agent can either jump 1 blocks or 2-3 blocks. This will occur in level 4. It will be interesting to discover how the agent will perform when we add more uncertainty into the map and how we can improve its performance by adjusting our parameter values(reward values, learning rate, discount rate, etc.). Moreover, we plan to add nondeterministic actions into our project. For example, the agent may have a 20% probability of jumping left as opposed to walking left, obviously with respective reward factors for each action. Also, by level 5, our moonshot case, we will add zombies that will patrol the map and force the agent to perform zombie avoidance. This will add more actions to our project. Some challenges we faced while solving our three levels was being able to find an optimal path within 150 trials. This took many attempts at adjusting our Q-learning algorithm and by assigning a very large reward factor towards jumping. We did this because our agent would continually try to jump on the level 1 map, which did not require jumping to be solved optimally. Given our experience so far, so challenges we will face in the future are implementing more actions into our project and performing zombie avoidance. We plan to adjust our reward values accordingly and improve upon our Q-Learning algorithm to solve an optimal path with minimal trials. If the project proceeds as planned our team should be able to solve a level 5 map on a moderate to large scale.